Histogrammes, étude statistique et incertitude-type de répétabilité¶
Comment tracer un histogramme, réaliser une étude statistique et calculer une incertitude-type de répétabilité (type A) sous Python?
code sous licence creative commun CC BY-NC-SA BY Gaëlle Rebolini
Lancer le notebook sur binder (lent)
Ceci est un petit tutoriel permettant de tracer des histogrammes, de déterminer une valeur moyenne, un écart-type et une incertitude-type de répétabilité (type A) à partir d’un échantillon de valeurs.
Voici un programme exploitant des mesures de volume réalisées à l’éprouvette graduée. On mesure le plus précisément possible 50 mL d’eau à l’aide d’une éprouvette graduée. Puis, on pèse cette eau et on en déduit par un simple calcul faisant intervenir la masse volumique, le volume d’eau correspondant avec une meilleure précision. On réalise la manipulation un grand nombre de fois, ce qui nous permet d’obtenir un échantillon de valeurs.
Dans un premier temps, vous est présenté le programme complet. Les lignes de code seront explicitées dans un second temps.
[1]:
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
Veprouvette =[49.61,49.55,50.91,50.87,48.03,50.29,48.58,48.06,50.06,50.72,48.95,49.4,49.21,49.31,49.78,48.77]
plt.figure(figsize=(12,10))
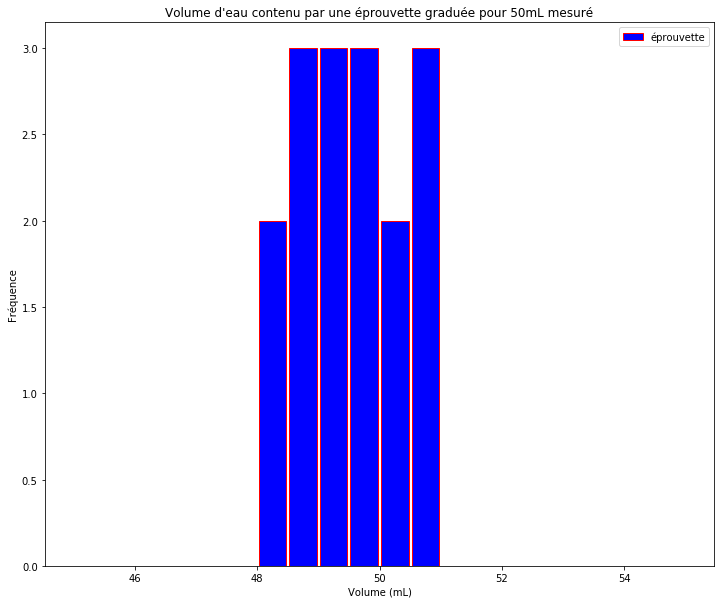
plt.hist(Veprouvette,bins=20,range=(45,55),align="mid",rwidth=0.9,color="b",edgecolor="red",label="éprouvette")
plt.title("Volume d'eau contenu par une éprouvette graduée pour 50mL mesuré")
plt.xlabel("Volume (mL)")
plt.ylabel("Fréquence")
plt.legend()
plt.show()
Vmoy=np.mean(Veprouvette)
ecarttype=np.std(Veprouvette)
effectif=len(Veprouvette)
incertitudetype=ecarttype/np.sqrt(effectif)
print("{0:55}".format("Le volume moyen :"),Vmoy,"mL")
print("{0:55}".format("L'écart-type vaut :"),ecarttype,"mL")
print("{0:55}".format("Le nombre de mesures vaut :"),effectif)
print("{0:55}".format("L'incertitude-type de répétabilité de deltat vaut :"),incertitudetype,"mL")
Le volume moyen : 49.506249999999994 mL
L'écart-type vaut : 0.8814042418209694 mL
Le nombre de mesures vaut : 16
L'incertitude-type de répétabilité de deltat vaut : 0.22035106045524236 mL
EXPLICATIONS DU PROGRAMME¶
Attention à bien exécuter les cellules de code suivantes les unes après les autres. Il est normal que rien ne s’affiche lors de l’exécution de certaines cellules.
Import des bibliothèques utiles¶
[2]:
import matplotlib.pyplot as plt # bibliothèque obligatoire pour créer des graphiques
import numpy as np # bibliothèque utile pour déterminer la valeur moyenne, l'écart-type
# et l'incertitude-type de répétabilité
Création de la liste contenant les valeurs de l’échantillon¶
Pour créer un histogramme puis réaliser l’étude statistique sous Python, il faut tout d’abord créer une liste contenant les valeurs de l’échantillon.
On peut aussi créer un tableau numpy grâce à la fonction np.array() de la bibliothèque numpy as np.
[3]:
Veprouvette =[49.61,49.55,50.91,50.87,48.03,50.29,48.58,48.06,50.06,50.72,48.95,49.4,49.21,49.31,49.78,48.77]
Comment créer et paramétrer un histogramme¶
On commence par créer une fenêtre graphique aux dimensions souhaitées grâce à la méthode plt.figure(num, figsize, dpi) de la bibliothèque matplotlib.pyplot as plt. Pour plus d’informations, se référer au notebook graphiques_partie_1.
Puis on crée l’histogramme à l’aide de la méthode plt.hist(x,bins,range,align,orientation,rwidth,log,color,edgecolor,label) de la bibliothèque matplotlib.pyplot as plt
Voici les principaux paramètres de cette méthode, sachant qu’il n’est pas obligatoire de tous les spécifier. Dans ce cas, ils prendront leur valeur par défaut. D’autres paramètres existent, pour plus d’informations : https://matplotlib.org/api/_as_gen/matplotlib.pyplot.hist.html?highlight=hist#matplotlib.pyplot.hist
x : tableau contenant les valeurs de l’échantillon
bins : le nombre d’intervalles donc de barres ; optionnel, la valeur par défaut est 10.
range : donne les valeurs limites de l’axe des abscisses (xmin,xmax) ; optionnel
align : {“left”, “mid”, “right”}; optionnel, La valeur par défaut est “mid”
'left': la barre est centrée sur le côté gauche de l'intervalle 'mid': la barre est centrée sur le centre de l'intervalle 'right': la barre est centrée sur le côté droit de l'intervalle
orientation : {“horizontal”, “vertical”}; optionnel, la valeur par défaut est “vertical”
rwidth : largeur des barres sous la forme d’une fraction de l’intervalle ; optionnel, la valeur par défaut est 1.
log : booléen, permet d’afficher une échelle logarithmique pour l’axe des abscisses si log=True ; optionnel, valeur par défaut :False
color : couleur des barres ; optionnel
edgecolor : couleur du contour des barres ; optionnel
label : permet de légender l’histogramme ; optionnel. Attention, son utilisation nécessite l’appel de la méthode plt.legend() dans la suite du programme
On peut ensuite afficher un titre, légender les axes de l’histogramme tout comme on le ferait sur un graphique grâce aux méthodes plt.title(), plt.xlabel(), plt.ylabel()… Enfin, on affiche l’histogramme grâce à la méthode plt.show().
Pour plus d’informations concernant ces dernières méthodes, se référer au notebook graphiques_partie_1.
Premier exemple : Utilisation de la méthode plt.hist() sans passage de paramètre¶
[4]:
plt.figure(figsize=(12,10))
plt.hist(Veprouvette)
plt.title("Volume d'eau contenu par une éprouvette graduée pour 50mL mesuré")
plt.xlabel("Volume (mL)")
plt.ylabel("Fréquence")
plt.show()
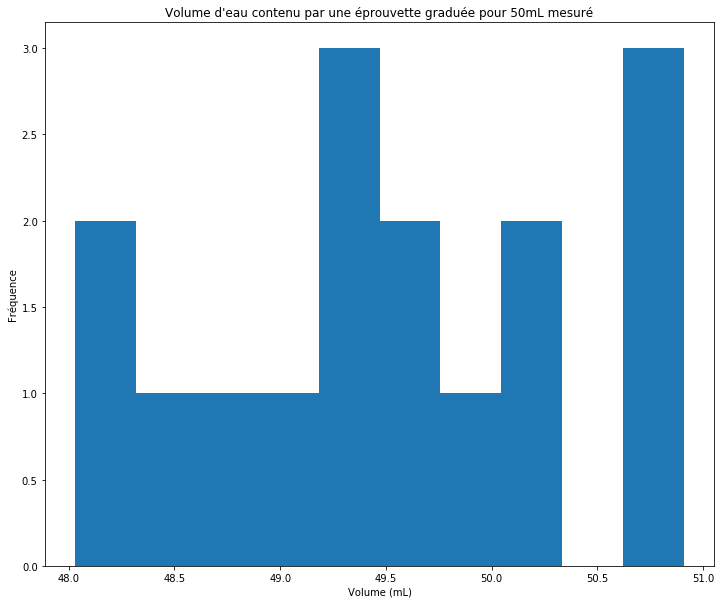
Deuxième exemple : Utilisation de la méthode plt.hist() avec passage de paramètres¶
[5]:
plt.figure(figsize=(12,10))
plt.hist(Veprouvette,bins=20,range=(45,55),align="mid",rwidth=0.9,color="y",edgecolor="r",label="éprouvette")
plt.title("Volume d'eau contenu par une éprouvette graduée pour 50mL mesuré")
plt.xlabel("Volume (mL)")
plt.ylabel("Fréquence")
plt.legend()
plt.show()
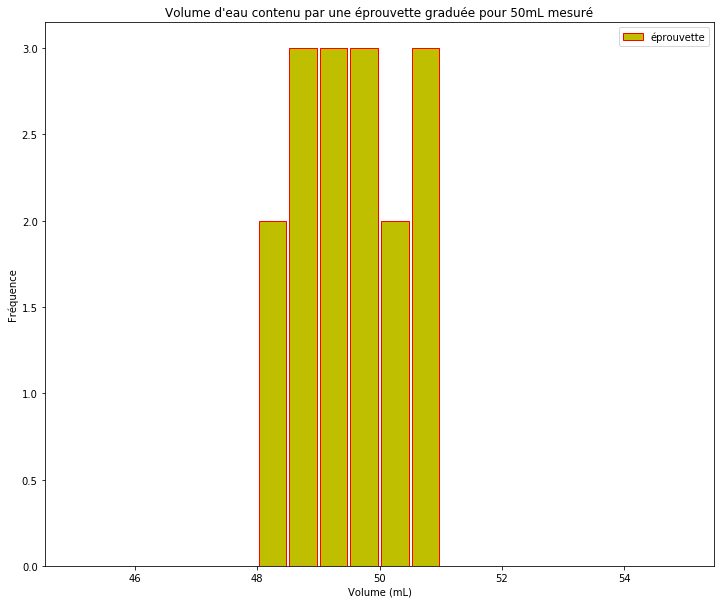
Et si l’on veut afficher plusieurs histogrammes dans la même fenêtre graphique?¶
Il suffit d’appeler la méthode plt.hist() autant de fois que nécessaire. Les paramètres sont alors très utiles!
[6]:
Vbecher=[50.65,48.26,47.83,47.76,50.26,47.23,43.88,43.92,48.69,48.66,43.67,47.53,49.55,50.64,43.8,48.53]
Veprouvette =[49.61,49.55,50.91,50.87,48.03,50.29,48.58,48.06,50.06,50.72,48.95,49.4,49.21,49.31,49.78,48.77]
Vfiole=[49.74,49.77,49.71,49.75,49.52,49.8,49.61,49.56,49.65,49.65,49.52,49.64,49.74,49.81,49.5,49.59]
plt.figure(figsize=(12,10))
plt.hist(Vbecher,bins=32,range=(43,51),align="left",rwidth=0.3,color="r",label="becher")
plt.hist(Veprouvette,bins=32,range=(43,51),align="mid",rwidth=0.3,color="b",label="éprouvette")
plt.hist(Vfiole,bins=32,range=(43,51),align="right",rwidth=0.3,color="g",label="fiole jaugée")
plt.title("Volume d'eau contenu par un bécher, une éprouvette graduée ou une fiole jaugée pour 50mL mesuré")
plt.xlabel("Volume (mL)")
plt.ylabel("Fréquence")
plt.legend()
plt.show()
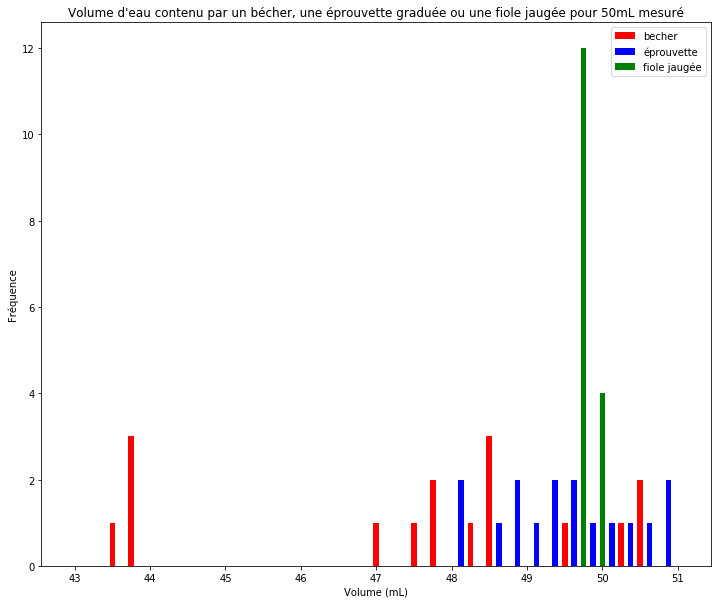
Détermination de la moyenne, de l’écart-type, de l’effectif et de l’incertitude-type de répétabilité (ou incertitude de type A)¶
On utilise les fonctions de la bibliothèque numpy as np:
la fonction np.mean(x) permet de calculer la valeur moyenne de l’échantillon x
la fonction np.std(x) permet de calculer l’écart-type de l’échantillon x
la fonction np.sqrt(a) permet de calculer la racine carrée du nombre a et sera utile lors du calcul de l’incertitude-type de répétabilité.
La fonction len(x) permet de calculer l’effectif (nombre de valeurs) de l’échantillon x.
Pour ces trois fonctions, x peut être un tableau, un p-uplet (tuple en anglais), un tableau numpy. Pour plus de renseignements sur les listes, tuples ou les tableaux numpy, se référer aux notebooks Listes et Tableaux numpy.
L’incertitude-type de répétabilité a pour formule \(U(x)=\frac{écart-type(x)}{\sqrt{effectif(x)}}\)
Attention, ce programme n’arrondit pas les valeurs et n’exprime pas avec le bon nombre de chiffres significatifs la valeur moyenne et l’incertitude-type.
[7]:
Vmoy=np.mean(Veprouvette)
ecarttype=np.std(Veprouvette)
effectif=len(Veprouvette)
incertitudetype=ecarttype/np.sqrt(effectif)
print("{0:55}".format("Le volume moyen :"),Vmoy,"mL")
print("{0:55}".format("L'écart-type vaut :"),ecarttype,"mL")
print("{0:55}".format("Le nombre de mesures vaut :"),effectif)
print("{0:55}".format("L'incertitude-type de répétabilité de deltat vaut :"),incertitudetype,"mL")
Le volume moyen : 49.506249999999994 mL
L'écart-type vaut : 0.8814042418209694 mL
Le nombre de mesures vaut : 16
L'incertitude-type de répétabilité de deltat vaut : 0.22035106045524236 mL