Les modélisations

Code sous licence creative commun CC BY-NC-SA BY Gaëlle Rebolini

Télécharger le pdf

Télécharger le notebook

Lancer le notebook sur binder (lent)

Dans ce tutoriel, on apprendra à modéliser un nuage de points.

Reprenons l’exemple de la loi d’Ohm (Tutoriel sur le tracé d’un graphique \(1^{ère}\) partie) et modélisons la courbe obtenue.

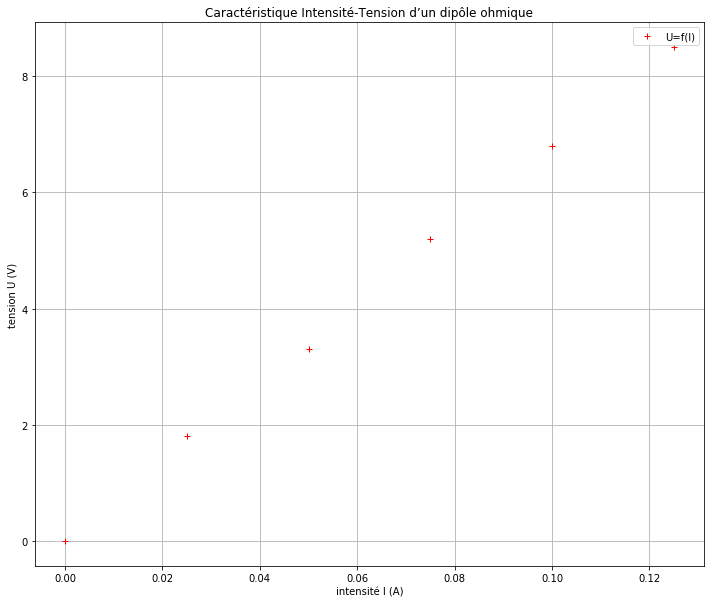
Affichons la courbe obtenue avant modélisation :

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

# tableaux numpy impératifs pour réaliser le calcul (vectorisé) de
# la tension modélisée Umodel lors de la modélisation ultérieure

I=np.array([0,25e-3,50e-3,75e-3,100e-3,125e-3])
U=np.array([0,1.8,3.3,5.2,6.8,8.5])

fig = plt.figure(figsize=(12,10))
plt.plot(I,U,'r+',label='U=f(I)')
plt.legend()
plt.xlabel("intensité I (A)")
plt.ylabel("tension U (V)")
plt.grid()
plt.title("Caractéristique Intensité-Tension d’un dipôle ohmique")
plt.show()

Première partie : Modélisation à l’aide de la fonction polyfit de la bibliothèque numpy

Si le nuage de points est modélisable par une fonction polynomiale, on peut utiliser la fonction np.polyfit( x , y , deg) de la bibliothèque numpy as np.

Le paramètre deg correspond au degré du polynôme.

La fonction polyfit retourne un tableau numpy à une dimension de coefficients p qui minimisent l’erreur à l’aide de la méthode des moindres carrés dans l’ordre : deg , deg-1 ,… 0

\(P(x) = p[0] \times x^{deg} + p[1] \times x^{deg-1}... + p[deg]\)

D’autres paramètres existent. Pour plus d’informations :

https://docs.scipy.org/doc/numpy-1.15.0/reference/generated/numpy.polyfit.html

Dans le cadre du programme de physique-chimie au lycée, on a besoin au plus de polynômes du second degré.

• Pour un polynôme de degré 2 : \(P(x)=p[0]\times x^2+p[1]\times x+p[2]\)

• Pour un polynôme de degré 1 : \(P(x)=p[0]\times x+p[1]\)

• Pour un polynôme de degré 0 : \(P(x)=p[0]\)

Modélisons maintenant la courbe obtenue par une droite (polynôme de degré 1) et affichons les coefficients :

coeff=np.polyfit(I, U,1)
print(coeff[0],coeff[1])

67.88571428571427 0.023809523809522625

Avec une décimale :

print ('{0:.1f}'.format(coeff[0]),'{0:.1f}'.format(coeff[1]))

67.9 0.0

Créons l’équation de la droite modélisée grâce à ces coefficients et affichons cette équation ainsi que son tableau de valeurs :

Umodel = coeff[0]*I+coeff[1]
print('U={0:.1f}'.format(coeff[0]),'xI+{0:.1f}'.format(coeff[1]))
print(Umodel)

U=67.9 xI+0.0
[0.02380952 1.72095238 3.41809524 5.1152381  6.81238095 8.50952381]

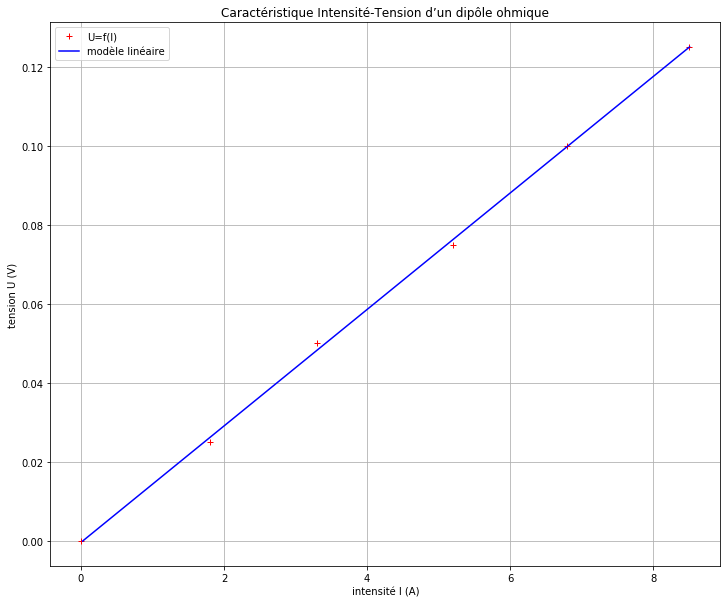
Affichons maintenant les points expérimentaux et la droite modélisée sur le même graphique :

NOTE CODAGE : “r+” à la ligne 2 permet d’afficher un + rouge pour chaque point expérimental alors que “b-“ à la ligne 3 permet de relier les points modélisés par des segments de droite bleus.

fig = plt.figure(figsize=(12,10))
plt.plot(U,I,'r+',label='U=f(I)')
plt.plot(Umodel,I,'b-',label='modèle linéaire')
plt.legend()
plt.xlabel("intensité I (A)")
plt.ylabel("tension U (V)")
plt.grid()
plt.title("Caractéristique Intensité-Tension d’un dipôle ohmique")
plt.show()

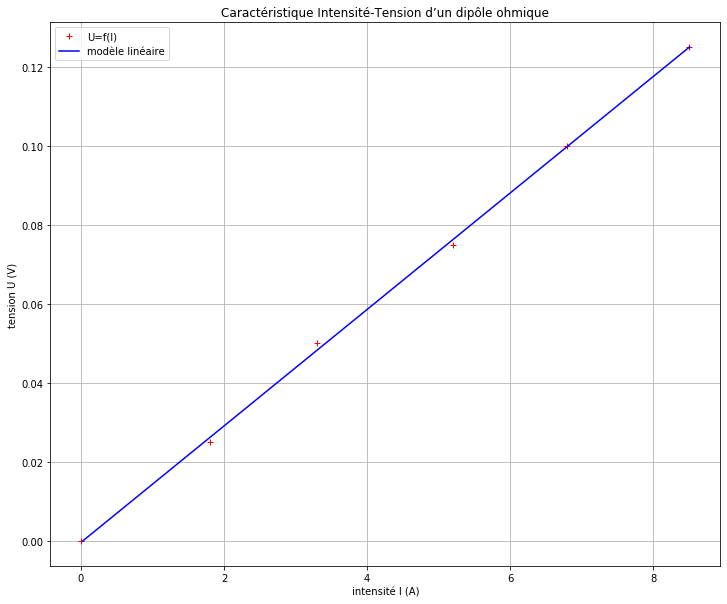
Voici le programme dans sa totalité afin d’y voir un peu plus clair !

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

I=np.array([0,25e-3,50e-3,75e-3,100e-3,125e-3])
U=np.array([0,1.8,3.3,5.2,6.8,8.5])

coeff=np.polyfit(I, U,1)
Umodel = coeff[0]*I+coeff[1]
print('U={0:.1f}'.format(coeff[0]),'xI+{0:.1f}'.format(coeff[1]))

fig = plt.figure(figsize=(12,10))
plt.plot(U,I,'r+',label='U=f(I)')
plt.plot(Umodel,I,'b-',label='modèle linéaire')
plt.legend()
plt.xlabel("intensité I (A)")
plt.ylabel("tension U (V)")
plt.grid()
plt.title("Caractéristique Intensité-Tension d’un dipôle ohmique")
plt.show()

U=67.9 xI+0.0

Deuxième partie : Modélisation à l’aide de la fonction linregress du module stats de la bibliothèque scipy

Afin de réaliser une régression linéaire, il est aussi possible d’utiliser la fonction linregress issue du module stats de la bibliothèque scipy :

slope, intercept, r_value, p_value, std_error = stats.linregress(x,y).

Cette fonction est un plus ardue d’utilisation pour des débutants mais permet d’obtenir la valeur du coefficient de corrélation. Elle retourne cinq variables dont seules les 3 premières sont utiles en spécialité physique : - slope : le coefficient directeur (ou pente) - intercept : l’ordonnée à l’origine - r_value : le coefficient de correlation - p_value : « valeur de p bilatérale pour un test d’hypothèse dont l’hypothèse nulle est que la pente est nulle » : cette valeur sera d’autant plus grande que la probabilité d’avoir une pente nulle est importante. Par contre, si la probabilité d’avoir une pente nulle est nulle, alors cette valeur sera nulle elle-aussi. - std_error : « Erreur standard d’estimation » : plus cette valeur est faible et plus l’estimation de la pente est précise.

Pour plus d’informations : https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.linregress.html

Modélisons maintenant la courbe obtenue par une droite et affichons les variables de sortie qui nous intéresse :

from scipy import stats
slope, intercept, r_value, p_value, std_error = stats.linregress(I,U)
print ('pente :',slope)
print ("ordonnée à l'origine :", intercept)
print ('coefficient de corrélation r :',r_value)

pente : 67.88571428571429
ordonnée à l'origine : 0.023809523809523725
coefficient de corrélation r : 0.999720478354276

Créons l’équation de la droite modélisée et affichons cette équation ainsi que son tableau de valeurs :

Umodel = slope*I+intercept
print ('U={0:.1f}'.format(slope),'xI+{0:.1f}'.format(intercept))
print(Umodel)

U=67.9 xI+0.0
[0.02380952 1.72095238 3.41809524 5.1152381  6.81238095 8.50952381]

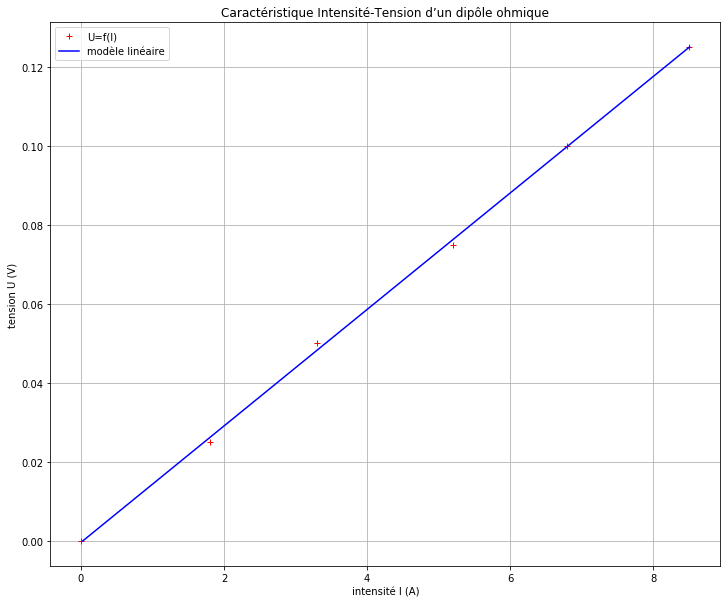
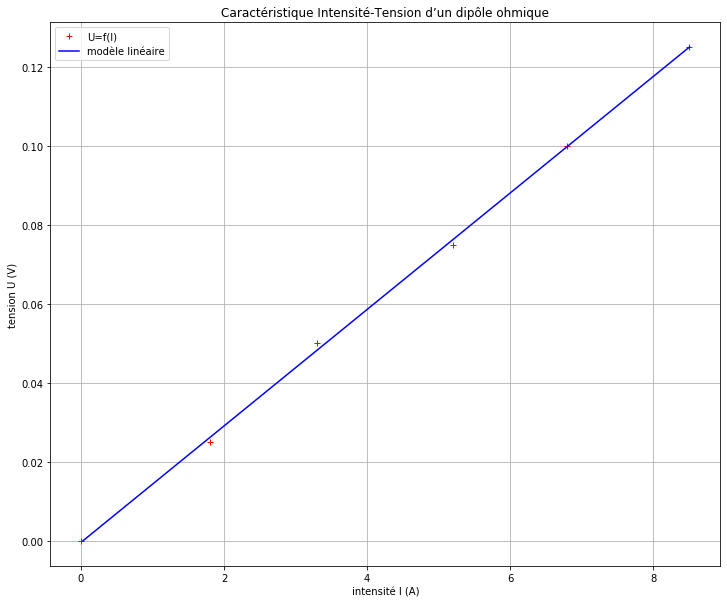
Affichons maintenant les points expérimentaux et la droite modélisée sur le même graphique :

fig = plt.figure(figsize=(12,10))
plt.plot(U,I,'r+',label='U=f(I)')
plt.plot(Umodel,I,'b-',label='modèle linéaire')
plt.legend()
plt.xlabel("intensité I (A)")
plt.ylabel("tension U (V)")
plt.grid()
plt.title("Caractéristique Intensité-Tension d’un dipôle ohmique")
plt.show()

Voici le programme dans sa totalité afin d’y voir un peu plus clair !

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
%matplotlib inline

I=np.array([0,25e-3,50e-3,75e-3,100e-3,125e-3])
U=np.array([0,1.8,3.3,5.2,6.8,8.5])

slope, intercept, r_value, p_value, std_error = stats.linregress(I,U)
Umodel = slope*I+intercept
print ('U={0:.1f}'.format(slope),'xI+{0:.1f}'.format(intercept))
print ('coefficient de corrélation r :',r_value)


fig = plt.figure(figsize=(12,10))
plt.plot(U,I,'r+',label='U=f(I)')
plt.plot(Umodel,I,'b-',label='modèle linéaire')
plt.legend()
plt.xlabel("intensité I (A)")
plt.ylabel("tension U (V)")
plt.grid()
plt.title("Caractéristique Intensité-Tension d’un dipôle ohmique")
plt.show()

U=67.9 xI+0.0
coefficient de corrélation r : 0.999720478354276