Les fonctions¶
code sous licence creative commun CC BY-NC-SA BY Dominique Devedeux
Lancer le notebook sur binder (lent)
Lorsqu’on écrit un programme, on a besoin de fonctions diverses et variées.
Les fonctions mathématiques arithmétiques (multiplication, addition,…) ou logiques (OU, ET, …) classiques sont accessibles dans la bibliothèque de « base » de python et ne recquièrent aucune ligne de code supplémentaire pour y avoir accès.
Les fonctions mathématiques plus sophistiquées sont inclues dans des bibliothèques spécifiques disponibles qu’il faut importer avant de pouvoir utiliser ces fonctions.
On peut aussi avoir besoin de créer ses propres fonctions personnalisées.
Une bibliothèque est donc un ensemble de fonctions prédéfinies.
Bibliothèques externes disponibles¶
Une des grandes forces du langage Python réside dans le nombre important de bibliothèques logicielles externes disponibles. Celles-ci sont mises à disposition afin de pouvoir être utilisées sans avoir à les réécrire.
Quelques exemples :
la librairie math contient entre autres les fonctions trigonométriques, la racine carrée, les recherches de PGCD, les factorielles …
la librairie random permet d’avoir accès à de nombreuses fonctions en rapport avec la génération de nombres aléatoires,
la librairie matplotlib contient toutes les fonctions permettant de générer et de gérer l’affichage de graphiques,
la librairie numpy contient de nombreux outils mathématiques (trigonométriques, tableaux,…) et permet entre autres de modéliser des ensembles de valeurs.
L’importation des bibliothèques doit se faire en tête de programme
Pour importer une bibliothèque, il suffit d’écrire la ligne : import nom_de_la_bibliothèque
L’accès à la fonction s’effectue ainsi : nom_de_la_bibliothèque.nom_de_la_fonction
On peut aussi donner un petit surnom à la bibliothèque par souci de simplification : import nom_de_la_bibliothèque as surnom
On peut aussi parfois ne vouloir importer qu’une fonction spécifique et non pas la totalité d’une bibliothèque. Il suffit alors d’écrire : from nom_de_la_bibliothèque import fonction. Attention dans ce cas, l’accés à la fonction s’effectue ainsi : nom_de_la_fonction
https://docs.python.org/fr/3/library/random.html
[1]:
# Importation de la bibliothèque math sans surnom
import math
print(math.cos(math.pi)) # permet d'avoir accès à la fonction cosinus ainsi qu'à la valeur de pi et d'afficher le résultat
-1.0
[2]:
# Importation de la bibliothèque random avec surnom
import random as rd
print(rd.randint(1,10)) # la fonction randint permet d'afficher à l'écran un nombre aléatoire entier compris entre 1 et 10
7
[3]:
# Importation de la seule fonction randint à partir de la bibliothèque random
from random import randint
print(randint(1,10)) # ne pas écrire random.randint() mais uniquement randint()
2
Fonctions personnalisées¶
Un programme écrit « linéairement » est peu lisible . On préfère en général le décomposer en plusieurs sous-programmes, nommés fonctions.
Une fonction est donc un ensemble d’instructions !
Les avantages de définir des fonctions sont multiples :
le programme est plus lisible car architecturé, et se comprend plus facilement ;
le code est réutilisable ;
le programme est moins long : il suffit de définir une fonction pour effectuer une tâche précise, puis appeler cette fonction plusieurs fois si nécessaire ;
le programme est plus facile à corriger et à améliorer.
Création d’une fonction¶
Les fonctions sont souvent écrites en tête de programme, après les imports de bibliothèques
La définition d’une fonction commence toujours par la ligne def nom_de_la_fonction(): (ne pas oublier les : à la fin, erreur classique)
Les lignes de codes de cette fonction sont ensuite écrites en-dessous avec une indentation (décalage vers la droite).
Lorsqu’il a besoin de cette fonction, le programme principal (PP) doit l’appeler : nom_de_la_fonction()
Le PP peut avoir besoin d’échanger des informations avec la fonction.
Il est conseillé de documenter la fonction en utilisant la syntaxe
""" (...) """juste après la déclaration de fonction
Les exemples ci-après sont progressifs. Les fonctions étudiées n’ont pas d’autre intérêt que d’illustrer les différents échanges possibles entre le PP et la fonction.
[4]:
#Dans ce premier exemple, il n'y a pas d'échange d'informations entre le PP et la fonction
# Définition de la fonction nommée félicitations
def félicitations() : # déclaration de la fonction
"""
Affiche un message de fécilicitations
"""
print("Bien joué !") # ligne de code de la fonction
#Programme principal
félicitations() # Appel de la fonction
Bien joué !
Dans ce second exemple, le PP envoie le texte à imprimer à la fonction. Le PP envoie donc un paramètre (ici la variable texte1) à la fonction qui le range dans sa propre variable texte. 
[5]:
# Définition de la fonction nommée affichage
def affichage(texte) : # la variable texte contiendra la variable envoyée par le PP
"""
Affichage du texte donné en argument
:param texte: texte à afficher
"""
print(texte)
#Programme principal
texte1 ="Bien joué !"
affichage(texte1) # Premier appel de la fonction avec envoi de la variable texte1
texte2 ="Perdu !"
affichage(texte2) # Second appel de la fonction avec envoi de la variable texte2
Bien joué !
Perdu !
Dans ce troisième exemple, le PP envoie deux paramètres (ici les variables a et b) à la fonction qui les range dans deux variables locales (ici x et y). Après avoir rempli son rôle, la fonction renvoie le résultat au PP. Celui-ci range alors le résultat dans sa variable res. 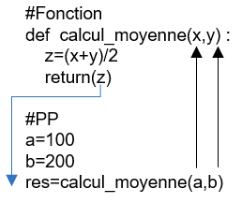
[6]:
# Définition de la fonction nommée calcul_moyenne
def calcul_moyenne(x,y) : # la variable x contiendra la valeur 100 et y contiendra la valeur 200
"""
Calcul de la moyenne de x et y
:param x: valeur x
:param y: valeur y
:return: moyenne de x et y
"""
z=(x+y)/2
return(z) # la fonction renvoie le résultat z au PP
#Programme principal
a=100
b=200
res=calcul_moyenne(a,b) # Appel de la fonction avec envoi de 2 variables a et b ET stockage du résultat
print(res) # renvoyé par la fonction dans la variable res.
150.0
Passage des arguments d’une fonction¶
La lecture du code et de la documentation d’une fonction est utile pour connaître l’ordre et la signification des arguments d’une fonction, cependant ce n’est pas toujours pratique au milieu d’un long programme de s’y reporter, surtout dans le cas de fonctions avec un grand nombre d’arguments.
Imaginons une fonction calculant la valeur du vecteur accélération moyen à partir des coordonnées de deux vecteurs vitesse \(\vec{v_1}\) et \(\vec{v_2}\) et de l’intervalle de temps \(\Delta t\)
On peut écrire cette fonction de plusieurs manières :
def calcul_acceleration(vx1, vy1, vz1, vx2, vy2, vy2, dt):
def calcul_acceleration(vx1, vx2, vy1, vy2, vz1, vz2, dt):
def calcul_acceleration(dt, vx1, vx2, vy1, vy2, vz1, vz2):
etc..
L’appel à la fonction en passant les arguments dans l’ordre nécessite de se rappeler quelle est la forme choisie pour l’ordre des arguments :
# pas très parlant...
calcul_acceleration(1, 0, 2, 3,0, 3, 0.04)
Heureusement, le python permet d’appeler une fonction en précisant le nom de chaque argument… et dans ce cas, il n’est plus nécessaire de donner les arguments dans l’ordre !
# beaucoup plus clair
calcul_acceleration(vx1=1, vy1=0, vz1=2, vx2=3, vy2=0, vz2=3, dt=0.04)
Mieux encore : il est possible de préciser dans la définition de la fonction des valeurs par défaut pour les arguments qui ne sont pas précisés lors de l’appel de la fonction.. si on travaille en 2 dimensions, par exemple, les valeurs en Z sont systématiquement nulles, on pert donc du temps à le préciser à chaque fois.
Il suffit alors de définir la fonction en précisant la valeur de chaque argument :
def calcul_acceleration(dt=0.04, vx1=0, vx2=0, vy1=0, vy2=0, vz1=0, vz2=0):
et l’appel de la fonction pour les vecteurs \(\vec{v_1}=(0,1,0)\) et \(\vec{v_2}=(1,0,0)\) pour l’intervalle « classique » de nos tables à coussin d’air \(\Delta t = 0.04\) se fait de la manière suivante :
calcul_acceleration(v1y=1, v2x=1)
[7]:
# Exemple complet
import math
def calcul_acceleration(dt=0.04, vx1=0, vx2=0, vy1=0, vy2=0, vz1=0, vz2=0):
"""
Calcul de l'accélération moyenne à partir des coordonnées de
deux vecteurs vitesse v1 et v2 et d'un intervalle de temps dt
:param dt: intervalle de temps en secondes (défaut : 0,04 s)
:param vx1: vecteur v1, coordonnée x (en mètres, défaut : 0 m)
:param vx2: vecteur v2, coordonnée x (en mètres, défaut : 0 m)
:param vy1: vecteur v1, coordonnée y (en mètres, défaut : 0 m)
:param vy2: vecteur v2, coordonnée y (en mètres, défaut : 0 m)
:param vz1: vecteur v1, coordonnée z (en mètres, défaut : 0 m)
:param vz2: vecteur v2, coordonnée z (en mètres, défaut : 0 m)
:return:
"""
return math.sqrt(((vx2-vx1)/dt)**2 + ((vy2-vy1)/dt)**2 + ((vz2-vz1)/dt)**2)
# Différentes manières d'appeler cette fonction
print("Calcul de l'accélération pour dt=1s, v1=(1,1,0) et v2=(2,0,0)")
# pas très clair, cauchemard de mémoire
print("Accélération : ", calcul_acceleration(1, 1, 2, 1, 0, 0, 0) , "m/s^2")
# peut être encore moins clair ?...
print("Accélération : ", calcul_acceleration(1, 1, 2, 1) , "m/s^2")
# mieux, non ?
print("Accélération : ", calcul_acceleration(vx1=1, vy1=1, vx2=2, dt=1), "m/s^2")
# on peut mixer les arguments par position et par nom
print("Accélération : ", calcul_acceleration(1, vx1=1, vy1=1, vx2=2) , "m/s^2")
Calcul de l'accélération pour dt=1s, v1=(1,1,0) et v2=(2,0,0)
Accélération : 1.4142135623730951 m/s^2
Accélération : 1.4142135623730951 m/s^2
Accélération : 1.4142135623730951 m/s^2
Accélération : 1.4142135623730951 m/s^2
Variables locales et globales (ou portée des variables)¶
Note : La portée d’une variable correspond aux parties du programme où la variable est définie.
Définitions¶
Une variable définie à l’intérieur d’une fonction est une variable locale. Elle ne sera pas reconnue au sein d’une autre fonction ni au sein du programme principal.
Une variable définie au niveau du programme principal est une variable globale. Elle est reconnue partout dans le programme, même au sein des fonctions.
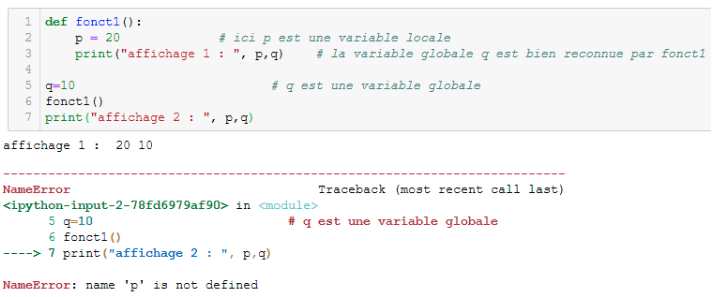
Le programme ci-dessous illustre ces deux premiers points :
la variable globale q est bien reconnue par la fonction qui peut ainsi l’afficher.
La variable locale p (définie au sein de la fonction) n’est pas reconnue dans le programme principal qui ne peut pas exécuter la demande d’affichage..
### Priorités
Lorsque des variables locales et globales sont définies par un même nom au sein d’un programme, elles obéissent à des règles de priorité :
au sein d’une fonction, ce sont les variables définies localement qui ont la priorité sur les variables globales. Ainsi, lors de l’exécution d’une fonction, c’est la valeur de la variable locale qui est prise en compte.
au sein du programme principal, une variable globale conserve sa valeur initiale même si elle a été modifiée au sein d’une fonction.
[8]:
def fonct1():
p = 20 # ici p est une variable locale qui prend la priorité
print("affichage 2 : p = ", p)
p=15 # ici p est une variable globale dont la valeur est 15
print("affichage 1 : p = ", p)
fonct1()
print("affichage 3 : p = ", p) # Au sein du programme principal, la variable globale p garde sa valeur initiale
affichage 1 : p = 15
affichage 2 : p = 20
affichage 3 : p = 15
Avantages des variables locales¶
Les variables locales permettent ainsi de compartimenter les actions. Cela signifie qu’un programme peut contenir quantités de fonctions sans se préoccuper le moins du monde des noms de variables qui y sont utilisées : en effet, ces variables étant locales (définies uniquement au sein d’une fonction), elles ne peuvent jamais interférer avec d’autres variables locales définies dans d’autres fonctions.
[9]:
def fonct1():
p = 20 # ici p est une variable locale
print("affichage 1 : p = ", p)
def fonct2():
p = 10 # ici p est une variable locale différente de celle créée dans fonct1
print("affichage 2 : p = ", p)
fonct1() # appel et exécution de la fonction fonct1
fonct2() # appel et exécution de la fonction fonct2
affichage 1 : p = 20
affichage 2 : p = 10
Conversion d’une variable locale en variable globale - inconvénients¶
On peut faire en sorte qu’une variable déclarée au sein d’une fonction soit malgré tout une variable globale. Pour cela, il suffit d’utiliser l’instruction global.
Remarque : il est cependant préférable d’éviter l’utilisation de l’instruction global car c’est une source d’erreurs (on peut ainsi modifier le contenu d’une variable globale en croyant agir sur une variable locale).
La sagesse recommande donc de suivre la règle suivante : ne jamais affecter dans une fonction une variable de même nom qu’une variable globale.
[10]:
def fonct1():
global p # ici p est une variable globale
p=20 # Notez l'absence de l'instruction return pour la variable globale!
def fonct2():
q=20 # ici q est une variable locale
# Notez l'absence de l'instruction return et sa conséquence en ligne 16-17!
def fonct3():
r=20 # ici r est une variable locale
return(r) # L'instruction return permet ici de renvoyer le contenu de la variable r au programmme principal
fonct1()
print("affichage 1 : p = ", p) # Au sein du programme principal, la variable globale p est bien reconnue alors qu'elle
# n'était définie qu'au sein de la fonction fonct1.
res2=fonct2()
print("affichage 2 : q = ", res2) # La fonction fonct2 ne renvoie rien et la variable q est locale à la fonct2 :
# La variable res2 ne contient donc aucune valeur !
res3=fonct3() # La fonction fonct3 renvoie le contenu de la variable r locale
print("affichage 2 : r = ", res3) # La variable res3 contient donc la valeur 20!
affichage 1 : p = 20
affichage 2 : q = None
affichage 2 : r = 20